Very frequently, we believe that an algorithm that performs a smaller number of operation is faster that another one; we usually follow this rule when optimizing our code. But this isn't always true, especially on RISC machines. It isn't unusual that we can improve the speed of an algorithm using a bigger number of simpler instructions, or performing calculations instead of reading them from a precalculated table.
As an example, we can consider an interpolation problem, frequently used in the resampling of signals or waveforms (like in samplers). For example, let's take a 4th order Lagrangian interpolator. If Xn are the waveform samples stored in memory, Y il the output sample, n is the integer part of the sample pointer, f is the fractional part of the sample pointer, this is the well known equation:

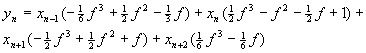
The classical approach to this problem is polyphase filtering. The fractional part f is quantized with N bits (generally between 12 and 16). For each possible value of f, the value of each polynomial coefficient is precalculated and stored into a table. During the resampling process, the fractional part of the pointer is taken and used as an index into the table for each sample; so the cost of the operation per sample is 4 multiplications, 3 additions and 4 table lookup. Some years ago this was the best solution, because an indexed access to a table was faster than many arithmetic calculations.
But now the situation is different: let’s take an average coefficient table, where values are stored as 32 bit float and N is 14: the size of this table is 256K. Besides, the accesses to the table are pseudo-random (cartainly are not sequential). The consequence is that the access to the table are all cache misses. With current processors, a cache miss correspond to a tens of clock cycles penality: so, what about computing the coefficient for all the samples, instead of reading them from a table? Following this way, we also improve the quality of the resampling, because we do not need to quantize the fractional part of the sample pointer. Well, using conventional scalar instructions we need 16 mul and 11 add (3 mul & 2 add for the first coeff, 3 mul & 3 add for the second coeff, 3 mul & 2 add for the third coeff, 3 mul & 1 add for the fourth coeff, 4 mul & 3 add for mutiply and add the samples and the coefficient). On modern pipelined processor (Pentium II or G3), this approach is only a little slower than reading the coefficients from the table.
But now we have another powerful possibility: SIMD instructions. Before reading the remaining part of this article, be sure to know the basics of SIMD instruction of Pentium III and Altivect processors; you can find documentation on Intel and Motorola web sites).
The trick that we can use is that all four coefficient are polynomials of degree 3, so they can be calculated using the same instructions. Now, multiple data with the same instructions = SIMD instructions. For illustration purposes only, I’m going to use a pseudo-Pentium III code; I think it should be easy to understand also for Altivect programmers.

Let’s call:
c3 = | -1/6 | 1/2 | -1/2 | 1/6 |
c2 = |  1/2 |  -1 |  1/2 |   0 |
c1 = | -1/3 |-1/2 |    1 |-1/6 |
c0 = |    0 |   0 |    1 |   0 |
F  = |    f |   f |    f |   f |

    movaps xmm0, c3
    mulps xmm0, F
    addps xmm0, c2
    mulps xmm0, F
    addps xmm0, c1
    mulps xmm0, F
    addps xmm0, c0
    mulps xmm0, [samples_pointer]

Now the xmm0 register contains the four samples x(n-1), x(n), x(n+1), x(n+2) multiplied by the corresponding coefficients; now we need to sum together these values in order to obtain the final result, but I omitted this piece of code because it is too processor dependent: Altivect has a single instruction that performs this operation, but on Pentium III processors you should shuffle and add. But on both processors this solution in much faster than reading the coefficient from a lookup table: it is 4 parallel multiplications and 4 parallel add instead of 4 scalar multiplications, 3 scalar additions and at least one cache miss. During our profiling test we noticed a 50% of speed-up. Not only: we measured a 12dB S/N ratio improvement, because the fractional part of the sample pointer isn't quantized. Finally, no giant (256K or more) tables are needed, so these memory can be used to store effective samples.